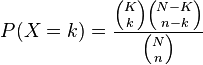- Power BI forums
- Updates
- News & Announcements
- Get Help with Power BI
- Desktop
- Service
- Report Server
- Power Query
- Mobile Apps
- Developer
- DAX Commands and Tips
- Custom Visuals Development Discussion
- Health and Life Sciences
- Power BI Spanish forums
- Translated Spanish Desktop
- Power Platform Integration - Better Together!
- Power Platform Integrations (Read-only)
- Power Platform and Dynamics 365 Integrations (Read-only)
- Training and Consulting
- Instructor Led Training
- Dashboard in a Day for Women, by Women
- Galleries
- Community Connections & How-To Videos
- COVID-19 Data Stories Gallery
- Themes Gallery
- Data Stories Gallery
- R Script Showcase
- Webinars and Video Gallery
- Quick Measures Gallery
- 2021 MSBizAppsSummit Gallery
- 2020 MSBizAppsSummit Gallery
- 2019 MSBizAppsSummit Gallery
- Events
- Ideas
- Custom Visuals Ideas
- Issues
- Issues
- Events
- Upcoming Events
- Community Blog
- Power BI Community Blog
- Custom Visuals Community Blog
- Community Support
- Community Accounts & Registration
- Using the Community
- Community Feedback
Register now to learn Fabric in free live sessions led by the best Microsoft experts. From Apr 16 to May 9, in English and Spanish.
- Power BI forums
- Galleries
- Quick Measures Gallery
- Hypergeometric Distribution Formula
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hypergeometric Distribution Formula
As explained here: https://www.statisticshowto.datasciencecentral.com/hypergeometric-distribution-examples/
The hypergeometric distribution is a probability distribution that’s very similar to the binomial distribution. In fact, the binomial distribution is a very good approximation of the hypergeometric distribution as long as you are sampling 5% or less of the population.
Therefore, in order to understand the hypergeometric distribution, you should be very familiar with the binomial distribution. Plus, you should be fairly comfortable with the combinations formula.
Hypergeometric Distribution Formula
The (somewhat formal) definition for the hypergeometric distribution, where X is a random variable, is:
This Quick Measure does the calculation above and has a bunch of error checking to boot.
Probability =
VAR __error = IF(ISBLANK(K[K Value]) || ISBLANK('k 2'[k Value 2]) || ISBLANK(N[N Value]) || ISBLANK([n Value 2]) || [n Value 2]<'k 2'[k Value 2] || K[K Value]<'k 2'[k Value 2] || N[N Value]<'n 2'[n Value 2] || N[N Value]<K[K Value],TRUE(),FALSE())
VAR __numerator = IF(__error,1,COMBIN(K[K Value],'k 2'[k Value 2])*COMBIN(N[N Value]-K[K Value],'n 2'[n Value 2]-'k 2'[k Value 2]))
VAR __demoninator = IF(__error,1,COMBIN(N[N Value],'n 2'[n Value 2]))
RETURN
IF(__error,"Bad Parameters",DIVIDE(__numerator,__demoninator,0))
eyJrIjoiZDFmMTk5NTYtZDFlNS00MWI4LTllOWMtMjc5MGYzYzVhMTNiIiwidCI6IjRhMDQyNzQzLTM3M2EtNDNkMi04MjdiLTAwM2Y0YzdiYTFlNSIsImMiOjN9
@ me in replies or I'll lose your thread!!!
Instead of a Kudo, please vote for this idea
Become an expert!: Enterprise DNA
External Tools: MSHGQM
YouTube Channel!: Microsoft Hates Greg
Latest book!: The Definitive Guide to Power Query (M)
DAX is easy, CALCULATE makes DAX hard...