- Power BI forums
- Updates
- News & Announcements
- Get Help with Power BI
- Desktop
- Service
- Report Server
- Power Query
- Mobile Apps
- Developer
- DAX Commands and Tips
- Custom Visuals Development Discussion
- Health and Life Sciences
- Power BI Spanish forums
- Translated Spanish Desktop
- Power Platform Integration - Better Together!
- Power Platform Integrations (Read-only)
- Power Platform and Dynamics 365 Integrations (Read-only)
- Training and Consulting
- Instructor Led Training
- Dashboard in a Day for Women, by Women
- Galleries
- Community Connections & How-To Videos
- COVID-19 Data Stories Gallery
- Themes Gallery
- Data Stories Gallery
- R Script Showcase
- Webinars and Video Gallery
- Quick Measures Gallery
- 2021 MSBizAppsSummit Gallery
- 2020 MSBizAppsSummit Gallery
- 2019 MSBizAppsSummit Gallery
- Events
- Ideas
- Custom Visuals Ideas
- Issues
- Issues
- Events
- Upcoming Events
- Community Blog
- Power BI Community Blog
- Custom Visuals Community Blog
- Community Support
- Community Accounts & Registration
- Using the Community
- Community Feedback
Register now to learn Fabric in free live sessions led by the best Microsoft experts. From Apr 16 to May 9, in English and Spanish.
- Power BI forums
- Community Blog
- Power BI Community Blog
- Linear Interpolation with Power BI
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
Introduction
If you are a mechanical engineer or mechanical engineering student, then you can skip past this introduction and the background information and just get right to the solution. I know this from my own experience in earning my Mechanical Engineering degree at Ohio Northern University. I had this professor, a Dr. Jed Marquart, for Thermodynamics and Fluid Mechanics. Nice enough guy, but looking back at it, probably a bit of a sadist. Homework, tests and final exams seemed like 75% of the time spent was on doing linear interpolation calculations. Misery...pure misery.
So, since I've been on this kick of demonstrating how to do some numerical methods and other math stuff in Power BI, I recalled the dozens, if not tens of thousands, of hours I spent as an undergraduate painstakingly doing linear interpolation to solve Thermodynamics and Fluid Mechanics problems. And I figured that perhaps, if I could save just one mechanical engineering student just a few tens of thousands of hours of linear interpolation time that it would be worth writing a blog article on how to do linear interpolation with Power BI. Besides, while we generally deal with known data in things like Power BI, having the ability to do interpolation could come in pretty handy for certain situations as well as "What If" analysis. So, here is the technique, but first a little background.
Background
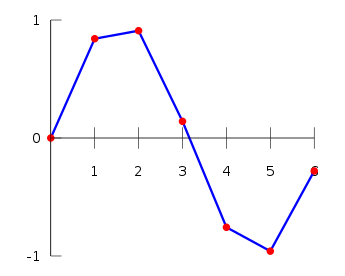
Interpolation falls into the mathematical field of numerical analysis. Essentially, interpolation is a method of creating new data points within the range of a set of known data points. So, for example, suppose we have a set of data points like the following for some unknown function f(x) (reference the Wikipedia page here😞
x f(x)
0 0
1 0 . 8415
2 0 . 9093
3 0 . 1411
4 −0 . 7568
5 −0 . 9589
6 −0 . 2794
But, what we are interested in is what the value of f(x) is for a value of x=2.5. How can we accomplish this? Well, we can assume that the values between our known values of f(x) approximately fall along a straight line, like so:
Using the two-point equation of a line, we get: y - y1 = m (x - x1), where m is the slope of the line. The slope of a line can be calculated with the formula m = (y2 - y1)/(x2 - x1). Thus, for x3 that is between x1 and x2, we get the final formula:
y3 = y1 + (x3 - x1) (y2 - y1)/(x2 - x1)
Plugging in our values we get:
y3 = .9093 + (2.5 - 2)(.1411-.9093)/(3-2)
y3 = .5252
So, you might be able to see how this could become a tad annoying if you had to do this 57 times in to solve a single Thermodynamics problem...
The Solution
Step 1: Get the Data
So, as a practical example of using interpolation, I chose to go grab some Thermodynamic steam tables from this site here. Specifically, this table. Now, to understand this data, these are tables of the properties of water at specific temperatures. These kinds of property tables are very common in Thermodynamics and Fluid Mechanics and come in both chart (diagram) and table form. For example, a Pressure-Enthalpy (P-h) diagram look like:
Nifty. But the problem is that not a single one of Dr. Marquart's problems EVER involved water at a temperature that was actually in these steam tables. Never. Not a single time. But I'm not bitter...
Deep breath. OK, so anyway, the data takes a little clean up, here is my Power Query code for cleaning up and importing the data. You will need to change the path in bold below for your own situation.
let
Source = Excel.Workbook(File.Contents("C:\temp\powerbi\Thermo\H2O_TempSat.xls"), null, true),
Sheet2 = Source{[Name="Sheet1"]}[Data],
#"Changed Type" = Table.TransformColumnTypes(Sheet2,{{"Column1", type text}, {"Column2", type text}, {"Column3", type text}, {"Column4", type text}, {"Column5", type text}, {"Column6", type text}, {"Column7", type text}, {"Column8", type text}, {"Column9", type text}, {"Column10", type text}, {"Column11", type text}, {"Column12", type text}, {"Column13", type text}}),
#"Removed Bottom Rows" = Table.RemoveLastN(#"Changed Type",2),
#"Removed Top Rows" = Table.Skip(#"Removed Bottom Rows",1),
#"Promoted Headers" = Table.PromoteHeaders(#"Removed Top Rows", [PromoteAllScalars=true]),
#"Changed Type1" = Table.TransformColumnTypes(#"Promoted Headers",{{" Temp", type text}, {" Pressure", type text}, {" volume (m^3/kg)", type text}, {"Column4", type text}, {" energy (kJ/kg)", type text}, {"Column6", type text}, {" enthalpy (kJ/kg)", type text}, {"Column8", type text}, {"Column9", type text}, {" entropy (kJ/kg.K)", type text}, {"Column11", type text}, {"Column12", type text}, {"Column13", type text}}),
#"Renamed Columns" = Table.RenameColumns(#"Changed Type1",{{" Temp", "Temp (C)"}, {" Pressure", "Pressure (MPa)"}, {" volume (m^3/kg)", "volume (m^3/kg) (vf)"}, {"Column4", "volume (m^3/kg) (vg)"}, {" energy (kJ/kg)", "energy (kJ/kg) (uf)"}, {"Column6", "energy (kJ/kg) (ug)"}, {" enthalpy (kJ/kg)", "enthalpy (kJ/kg) (hf)"}, {"Column8", "enthalpy (kJ/kg) (hfg)"}, {"Column9", "enthalpy (kJ/kg) (hg)"}, {" entropy (kJ/kg.K)", "entropy (kJ/kg.K) (sf)"}, {"Column11", "entropy (kJ/kg.K) (sfg)"}, {"Column12", "entropy (kJ/kg.K) (sg)"}}),
#"Removed Columns" = Table.RemoveColumns(#"Renamed Columns",{"Column13"}),
#"Removed Top Rows1" = Table.Skip(#"Removed Columns",1),
#"Changed Type2" = Table.TransformColumnTypes(#"Removed Top Rows1",{{"Temp (C)", type number}, {"Pressure (MPa)", type number}, {"volume (m^3/kg) (vf)", type number}, {"volume (m^3/kg) (vg)", type number}, {"energy (kJ/kg) (uf)", type number}, {"energy (kJ/kg) (ug)", type number}, {"enthalpy (kJ/kg) (hf)", type number}, {"enthalpy (kJ/kg) (hfg)", type number}, {"enthalpy (kJ/kg) (hg)", type number}, {"entropy (kJ/kg.K) (sf)", type number}, {"entropy (kJ/kg.K) (sfg)", type number}, {"entropy (kJ/kg.K) (sg)", type number}})
in
#"Changed Type2"
Step 2: Create Interpolation Table
OK, so what you should have loaded into a table now are the properties of water at temperatures in increments of 5 degrees Celsius from about 0 degrees to about 373 degrees. I named my table H2OTempSat.
Next, we want to create a table for our Interpolated values. You can do this by going to the Modeling tab of the ribbon and choosing New Parameter from the What If section or just click on New Table and use the following formula:
Interpolation = GENERATESERIES(1,373,1)
You should now have an Interpolation table with numbers from 1 to 373 in increments of 1. Rename the single column in the table to Temp (C).
Step 3: Create Interpolation Measure
Note that there is no reason to relate these tables to one another. In fact, I would advise against it, although I have specifically engineered the formula to allow for active relationships between your interpolation table and the lookup table. In any event, create the following measusre:
Pressure (MPa) =
VAR x3 = MAX(Interpolation[Temp (C)])
VAR match = CALCULATE(MAX(H2OTempSat[Pressure (MPa)]),FILTER(ALL(H2OTempSat),[Temp (C)]=x3))
VAR x1 = CALCULATE(MAX(H2OTempSat[Temp (C)]),FILTER(ALL(H2OTempSat),[Temp (C)]<=x3))
VAR x2 = CALCULATE(MIN(H2OTempSat[Temp (C)]),FILTER(ALL(H2OTempSat),[Temp (C)]>=x3))
VAR y1 = CALCULATE(MAX(H2OTempSat[Pressure (MPa)]),FILTER(ALL(H2OTempSat),[Temp (C)]<=x3))
VAR y2 = CALCULATE(MIN(H2OTempSat[Pressure (MPa)]),FILTER(ALL(H2OTempSat),[Temp (C)]>=x3))
RETURN IF(NOT(ISBLANK(match)),match,y1 + (x3 - x1) * (y2 - y1)/(x2 - x1))
So, what this measure is doing is calculating the Pressure (MPa) from our steam table by interpolating between the known values of pressure at the specific temperatures listed in our steam table. Line by line:
- The first line is just grabbing the value of the Temperature from our Interpolation table for which we want to interpolate a value for Pressure.
- The second line is looking to see if there is a match in the lookup table for the value that we have for our temperature. In other words, we will not have to interpolate a value, we already know it even though this would never happen in an Dr. Marquart classroom.
- The third line grabs the temperature in the steam table that is just below the value we have for our temperature.
- The fourth line grabs the temperature in the steam table that is just above the value we have for our temperature.
- The fifth line grabs the pressure in the steam table for the temperature that is just below the value we have for our temperature.
- The sixth line grabs the pressure in the steam table for the temperature that is just above the value we have for our temperature.
- The last line checks to see if we have a match in our steam table, and if so just returns the matched value. Otherwise, it performs the linear interpolation calculation.
Note the use of the ALL function within the FILTER function. This is the reason that we can handle relationships between our interpolation table and our lookup table.
Step 4: Create the Report
We can now easily create a simple report to show our interpolation results. First, create a Bubble Chart of Temp (C) and Pressure (MPa) from our original table, H2OTempSat. Then, create a second Bubble Chart of Temp (C) and Pressure (MPa) from our Interpolation table.
We should end up with something like the report below:
As one can clearly see, the interpolated values for Pressure (MPa) neatly fill in the gaps from our original table.
Conclusion
Dr. Marquart was a sadist.
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.
- Dynamic rollback of the previous N weeks of data
- Supercharge Your Visuals: Easy Conditional Formatt...
- The using of Cartesian products in many-to-many re...
- How to Filter similar Columns Based on Specific Co...
- Power BI Dynamic Date Filters: Automatically Updat...
- Enhanced Data Profiling in Power Query: GUI and Ta...
- How to use Tooltip to display breakdown data for a...
- Unveiling the Power of Lakehouse's SQL Analytics E...
- [DAX] Time Intelligence vs WINDOW vs OFFSET
- Display data in a fixed order and show data for th...
- joseftantawi on: How to customize open-sourced custom visual.
- kalpeshdangar on: Creating Custom Calendars for Accurate Working Day...
- gwayne on: Embracing TMDL Functionalities in Power BI and Pre...
- jian123 on: Sharing Power Query tables
-
 Martin_D
on:
From the Desk of An Experienced Power BI Analyst
Martin_D
on:
From the Desk of An Experienced Power BI Analyst
-
 ibarrau
on:
[PowerQuery] Catch errors in a request http
ibarrau
on:
[PowerQuery] Catch errors in a request http
- Aditya07 on: How to import customised themes in Power BI - usin...
-
 Martin_D
on:
Currency Conversion in Power BI: Enabling Seamless...
Martin_D
on:
Currency Conversion in Power BI: Enabling Seamless...
-
 technolog
on:
Unveiling Top Products with categories: A Guide to...
technolog
on:
Unveiling Top Products with categories: A Guide to...
-
 Ritaf1983
on:
When Big Numbers Become Big Problems
Ritaf1983
on:
When Big Numbers Become Big Problems
-
How To
573 -
Tips & Tricks
526 -
Support insights
121 -
Events
107 -
DAX
66 -
Power BI
65 -
Opinion
64 -
Power Query
62 -
Power BI Desktop
40 -
Power BI Dev Camp
36 -
Roundup
31 -
Power BI Embedded
20 -
Time Intelligence
19 -
Tips&Tricks
18 -
PowerBI REST API
12 -
Power Query Tips & Tricks
8 -
finance
8 -
Power BI Service
8 -
Direct Query
7 -
Power BI REST API
6 -
Auto ML
6 -
financial reporting
6 -
Data Analysis
6 -
Power Automate
6 -
Data Visualization
6 -
Python
6 -
Featured User Group Leader
5 -
Dax studio
5 -
Income Statement
5 -
powerbi
5 -
service
5 -
Power BI PowerShell
5 -
Machine Learning
5 -
community
4 -
RLS
4 -
M language
4 -
External tool
4 -
Paginated Reports
4 -
Power BI Goals
4 -
PowerShell
4 -
Desktop
4 -
Bookmarks
4 -
Group By
4 -
Line chart
4 -
Data Science
3 -
Azure
3 -
Conditional Formatting
3 -
Data model
3 -
Visualisation
3 -
Administration
3 -
M code
3 -
SQL Server 2017 Express Edition
3 -
Visuals
3 -
R script
3 -
Aggregation
3 -
Dataflow
3 -
calendar
3 -
Gateways
3 -
R
3 -
M Query
3 -
R visual
3 -
CALCULATE
3 -
Webinar
3 -
Reports
3 -
PowerApps
3 -
Incremental Refresh
2 -
Query Plans
2 -
Power BI & Power Apps
2 -
Random numbers
2 -
Day of the Week
2 -
Tips and Tricks
2 -
Number Ranges
2 -
M
2 -
hierarchies
2 -
Power BI Anniversary
2 -
Language M
2 -
VLOOKUP
2 -
pivot
2 -
calculated column
2 -
Power BI Premium Per user
2 -
Custom Visual
2 -
inexact
2 -
Date Comparison
2 -
Split
2 -
Forecasting
2 -
REST API
2 -
Editor
2 -
Working with Non Standatd Periods
2 -
powerbi.tips
2 -
Custom function
2 -
Reverse
2 -
measure
2 -
Microsoft-flow
2 -
Paginated Report Builder
2 -
PUG
2 -
Custom Measures
2 -
Filtering
2 -
Row and column conversion
2 -
Python script
2 -
Nulls
2 -
DVW Analytics
2 -
Industrial App Store
2 -
Week
2 -
Date duration
2 -
parameter
2 -
Weekday Calendar
2 -
Support insights.
2 -
construct list
2 -
Formatting
2 -
Power Platform
2 -
Workday
2 -
external tools
2 -
slicers
2 -
SAP
2 -
RANKX
2 -
Integer
2 -
index
2 -
PBI Desktop
2 -
Date Dimension
2 -
Power BI Challenge
2 -
Query Parameter
2 -
Visualization
2 -
Tabular Editor
2 -
SharePoint
2 -
Power BI Installation and Updates
2 -
How Things Work
2 -
troubleshooting
2 -
Date DIFF
2 -
Transform data
2 -
Date
2 -
rank
2 -
ladataweb
2 -
Sameperiodlastyear
1 -
Office Theme
1 -
matrix
1 -
bar chart
1 -
Measures
1 -
powerbi argentina
1 -
Model Driven Apps
1 -
REMOVEFILTERS
1 -
XMLA endpoint
1 -
translations
1 -
OSI pi
1 -
Parquet
1 -
Change rows to columns
1 -
remove spaces
1 -
Azure AAD
1 -
Governance
1 -
Fun
1 -
Power BI gateway
1 -
gateway
1 -
Elementary
1 -
Custom filters
1 -
Vertipaq Analyzer
1 -
powerbi cordoba
1 -
DIisconnected Tables
1 -
Sandbox
1 -
Honeywell
1 -
Combine queries
1 -
X axis at different granularity
1 -
ADLS
1 -
Primary Key
1 -
Microsoft 365 usage analytics data
1 -
Randomly filter
1 -
Week of the Day
1 -
Get latest sign-in data for each user
1 -
Retail
1 -
Power BI Report Server
1 -
School
1 -
Cost-Benefit Analysis
1 -
ISV
1 -
Ties
1 -
unpivot
1 -
Practice Model
1 -
Continuous streak
1 -
ProcessVue
1 -
Create function
1 -
Table.Schema
1 -
Acknowledging
1 -
Postman
1 -
Text.ContainsAny
1 -
Power BI Show
1 -
query
1 -
Dynamic Visuals
1 -
KPI
1 -
Intro
1 -
Icons
1 -
Issues
1 -
function
1 -
stacked column chart
1 -
ho
1 -
ABB
1 -
KNN algorithm
1 -
List.Zip
1 -
optimization
1 -
Artificial Intelligence
1 -
Map Visual
1 -
Text.ContainsAll
1 -
Tuesday
1 -
API
1 -
Kingsley
1 -
Merge
1 -
variable
1 -
financial reporting hierarchies RLS
1 -
Featured Data Stories
1 -
MQTT
1 -
Custom Periods
1 -
Partial group
1 -
Reduce Size
1 -
FBL3N
1 -
Wednesday
1 -
help
1 -
group
1 -
Scorecard
1 -
Json
1 -
Tops
1 -
Multivalued column
1 -
pipeline
1 -
Path
1 -
Yokogawa
1 -
Dynamic calculation
1 -
Data Wrangling
1 -
native folded query
1 -
transform table
1 -
UX
1 -
Cell content
1 -
General Ledger
1 -
Thursday
1 -
Quick Tips
1 -
data
1 -
PBIRS
1 -
Usage Metrics in Power BI
1 -
HR Analytics
1 -
keepfilters
1 -
Connect Data
1 -
Financial Year
1 -
Schneider
1 -
dynamically delete records
1 -
Copy Measures
1 -
Friday
1 -
Power Pivot
1 -
Natural Query Language
1 -
Infographic
1 -
automation
1 -
Prediction
1 -
newworkspacepowerbi
1 -
Performance KPIs
1 -
Active Employee
1 -
Custom Date Range on Date Slicer
1 -
refresh error
1 -
PAS
1 -
certain duration
1 -
DA-100
1 -
bulk renaming of columns
1 -
Single Date Picker
1 -
Monday
1 -
PCS
1 -
Saturday
1 -
Table
1 -
Custom Visuals
1 -
Free vs Pro
1 -
Format
1 -
Current Employees
1 -
date hierarchy
1 -
relationship
1 -
SIEMENS
1 -
Multiple Currency
1 -
Power BI Premium
1 -
On-premises data gateway
1 -
Binary
1 -
Power BI Connector for SAP
1 -
Sunday
1 -
Q&A
1 -
Event
1 -
Slicer
1 -
Visual
1 -
forecast
1 -
Regression
1 -
CICD
1 -
sport statistics
1 -
Intelligent Plant
1 -
Circular dependency
1 -
GE
1 -
Exchange rate
1 -
Dendrogram
1 -
range of values
1 -
activity log
1 -
Decimal
1 -
Charticulator Challenge
1 -
Field parameters
1 -
update
1 -
Announcement
1 -
Features
1 -
domain
1 -
pbiviz
1 -
Color Map
1 -
Industrial
1 -
Weekday
1 -
Working Date
1 -
Space Issue
1 -
Emerson
1 -
Date Table
1 -
Cluster Analysis
1 -
Stacked Area Chart
1 -
union tables
1 -
Number
1 -
Start of Week
1 -
Tips& Tricks
1 -
Training
1 -
deployment
1 -
ssrs traffic light indicators
1 -
SQL
1 -
trick
1 -
Scripts
1 -
Extract
1 -
Topper Color On Map
1 -
Historians
1 -
context transition
1 -
Custom textbox
1 -
OPC
1 -
Zabbix
1 -
Label: DAX
1 -
Business Analysis
1 -
Supporting Insight
1 -
rank value
1 -
Synapse
1 -
End of Week
1 -
Tips&Trick
1 -
Theme Colours
1 -
Text
1 -
Flow
1 -
Publish to Web
1 -
patch
1 -
Top Category Color
1 -
A&E data
1 -
Previous Order
1 -
Substring
1 -
Wonderware
1 -
Power M
1 -
Format DAX
1 -
Custom functions
1 -
accumulative
1 -
DAX&Power Query
1 -
Premium Per User
1 -
GENERATESERIES
1 -
Workspace
1 -
custom connector
1 -
Waterfall Chart
1 -
Power BI On-Premise Data Gateway
1 -
step by step
1 -
Top Brand Color on Map
1 -
Tutorial
1 -
Previous Date
1 -
XMLA End point
1 -
color reference
1 -
Date Time
1 -
Marker
1 -
Lineage
1 -
CSV file
1 -
conditional accumulative
1 -
Matrix Subtotal
1 -
Check
1 -
null value
1 -
Showcase
1 -
Report Server
1 -
Audit Logs
1 -
analytics pane
1 -
mahak
1 -
pandas
1 -
Networkdays
1 -
Button
1 -
Dataset list
1 -
Keyboard Shortcuts
1 -
Fill Function
1 -
LOOKUPVALUE()
1 -
Tips &Tricks
1 -
Plotly package
1 -
refresh M language Python script Support Insights
1 -
Cumulative Totals
1 -
Report Theme
1 -
Bookmarking
1 -
oracle
1 -
Canvas Apps
1 -
total
1 -
Filter context
1 -
Difference between two dates
1 -
get data
1 -
OSI
1 -
Query format convert
1 -
ETL
1 -
Json files
1 -
Merge Rows
1 -
CONCATENATEX()
1 -
take over Datasets;
1 -
Networkdays.Intl
1 -
Get row and column totals
1 -
Excel
1