- Power BI forums
- Updates
- News & Announcements
- Get Help with Power BI
- Desktop
- Service
- Report Server
- Power Query
- Mobile Apps
- Developer
- DAX Commands and Tips
- Custom Visuals Development Discussion
- Health and Life Sciences
- Power BI Spanish forums
- Translated Spanish Desktop
- Power Platform Integration - Better Together!
- Power Platform Integrations (Read-only)
- Power Platform and Dynamics 365 Integrations (Read-only)
- Training and Consulting
- Instructor Led Training
- Dashboard in a Day for Women, by Women
- Galleries
- Community Connections & How-To Videos
- COVID-19 Data Stories Gallery
- Themes Gallery
- Data Stories Gallery
- R Script Showcase
- Webinars and Video Gallery
- Quick Measures Gallery
- 2021 MSBizAppsSummit Gallery
- 2020 MSBizAppsSummit Gallery
- 2019 MSBizAppsSummit Gallery
- Events
- Ideas
- Custom Visuals Ideas
- Issues
- Issues
- Events
- Upcoming Events
- Community Blog
- Power BI Community Blog
- Custom Visuals Community Blog
- Community Support
- Community Accounts & Registration
- Using the Community
- Community Feedback
Register now to learn Fabric in free live sessions led by the best Microsoft experts. From Apr 16 to May 9, in English and Spanish.
- Power BI forums
- Community Blog
- Power BI Community Blog
- Combinatorics in Power Query -part1
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
Combinatorics is one of the most important areas of data analysis. It helps in painting a meaningful picture from tons of data very quickly.
We are often faced with a situation when we need to quickly detemine which combination of factors are actually driving the subtotal. In order to know that, it is important to generate all the subsets of a set and perform aggregation by those combinations in order to answer that question.
It is possible to generate all possible combinations of items in PowerBI using Power query and this post focuses on how to do that.
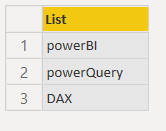
To elaborate, let's suppose there is a list as following
let
Source = {"powerBI","powerQuery","DAX"}
in
Source
and the end goal is to generate all possible subsets of this set which would be following
{},
{"powerBI"},{"powerQuery"},{"DAX"},
{"powerBI","powerQuery"},{"powerQuery","DAX"},{"powerBI","DAX"},
{"powerBI","powerQuery","DAX"}
The following code generates all possible subsets of this set.
let
Source = {"powerBI","powerQuery","DAX"}
p1 = List.Transform({1 .. Number.Power(2, List.Count(Source))}, each _ - 1),
#"Converted to Table" = Table.FromList(p1, Splitter.SplitByNothing(), {"Value"}),
#"Added Custom" = Table.AddColumn(
#"Converted to Table",
"Custom",
each
let
Loop = List.Generate(
() =>
[i = [Value], j = Number.IntegerDivide(i, 2), k = Number.Mod(i, 2), l = Text.From(k)],
each [i] > 0,
each [
i = [j],
j = Number.IntegerDivide(i, 2),
k = Number.Mod(i, 2),
l = Text.From(k) & [l]
],
each [l]
),
y = try Loop{List.Count(Loop) - 1} otherwise "0",
z = Text.PadStart(y, List.Count(Source), "0")
in
z
),
#"Added Custom1" = Table.AddColumn(#"Added Custom", "Custom.1", each Text.ToList([Custom])),
#"Added Custom2" = Table.AddColumn(
#"Added Custom1",
"Custom.2",
each
let
x = [Custom.1],
Terminate = List.Count(x),
Loop = List.Generate(
() => [i = 0, j = x{i}, k = if j = "1" then Source{i} else null],
each [i] < Terminate,
each [i = [i] + 1, j = x{i}, k = if j = "1" then Source{i} else null],
each [k]
)
in
List.RemoveNulls(Loop)
),
#"Added Custom3" = Table.AddColumn(
#"Added Custom2",
"Combinations",
each
let
x = [Custom.2],
y = List.Generate(
() => [i = 0, j = x{i}, k = j],
each [i] < List.Count(x),
each [i = [i] + 1, j = x{i}, k = [k] & "," & j],
each [k]
)
in
try y{List.Count(y) - 1} otherwise null
),
Combinations = #"Added Custom3"[Combinations]
in
Combinations
The code starts from here
and generates this
An optimized version of the above code is following
let
Source = {"powerBI","powerQuery","DAX"},
Initiator={{}},
Loop = List.Generate(
()=>[i=0,j=Source{i},k=List.Combine({Initiator{i},{j}}),l=List.InsertRange(Initiator,List.Count(Initiator),{k})],
each[i]<List.Count(Source),
each[i=[i]+1,j=Source{i},k=[l],l=
let x = List.Generate(
()=>[a=0,b=k{a},c=List.Combine({b,{j}}),d=List.Combine({k,{c}})],
each [a]<List.Count(k),
each [a=[a]+1,b=k{a},c=List.Combine({b,{j}}),d=List.Combine({[d],{c}})],
each[d] ) in x{List.Count(x)-1}],
each [l]
)
in
List.Transform(Loop{List.Count(Loop)-1},each Text.Combine(_,","))
A parameterized version with the choice a different delimiter is avaialble here
In my next post, I will show how this concept applies to a real-life scenario.
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.
- Dynamic rollback of the previous N weeks of data
- Supercharge Your Visuals: Easy Conditional Formatt...
- The using of Cartesian products in many-to-many re...
- How to Filter similar Columns Based on Specific Co...
- Power BI Dynamic Date Filters: Automatically Updat...
- Enhanced Data Profiling in Power Query: GUI and Ta...
- How to use Tooltip to display breakdown data for a...
- Unveiling the Power of Lakehouse's SQL Analytics E...
- [DAX] Time Intelligence vs WINDOW vs OFFSET
- Display data in a fixed order and show data for th...
- joseftantawi on: How to customize open-sourced custom visual.
- kalpeshdangar on: Creating Custom Calendars for Accurate Working Day...
- gwayne on: Embracing TMDL Functionalities in Power BI and Pre...
- jian123 on: Sharing Power Query tables
-
 Martin_D
on:
From the Desk of An Experienced Power BI Analyst
Martin_D
on:
From the Desk of An Experienced Power BI Analyst
-
 ibarrau
on:
[PowerQuery] Catch errors in a request http
ibarrau
on:
[PowerQuery] Catch errors in a request http
- Aditya07 on: How to import customised themes in Power BI - usin...
-
 Martin_D
on:
Currency Conversion in Power BI: Enabling Seamless...
Martin_D
on:
Currency Conversion in Power BI: Enabling Seamless...
-
 technolog
on:
Unveiling Top Products with categories: A Guide to...
technolog
on:
Unveiling Top Products with categories: A Guide to...
-
 Ritaf1983
on:
When Big Numbers Become Big Problems
Ritaf1983
on:
When Big Numbers Become Big Problems
-
How To
573 -
Tips & Tricks
526 -
Support insights
121 -
Events
107 -
DAX
66 -
Power BI
65 -
Opinion
64 -
Power Query
62 -
Power BI Desktop
40 -
Power BI Dev Camp
36 -
Roundup
31 -
Power BI Embedded
20 -
Time Intelligence
19 -
Tips&Tricks
18 -
PowerBI REST API
12 -
Power BI Service
8 -
Power Query Tips & Tricks
8 -
finance
8 -
Direct Query
7 -
Data Visualization
6 -
Python
6 -
Power BI REST API
6 -
Auto ML
6 -
financial reporting
6 -
Data Analysis
6 -
Power Automate
6 -
Machine Learning
5 -
Featured User Group Leader
5 -
Dax studio
5 -
Income Statement
5 -
powerbi
5 -
service
5 -
Power BI PowerShell
5 -
Desktop
4 -
Bookmarks
4 -
Group By
4 -
Line chart
4 -
community
4 -
RLS
4 -
M language
4 -
External tool
4 -
Paginated Reports
4 -
Power BI Goals
4 -
PowerShell
4 -
PowerApps
3 -
Data Science
3 -
Azure
3 -
Data model
3 -
Conditional Formatting
3 -
Visualisation
3 -
Administration
3 -
M code
3 -
SQL Server 2017 Express Edition
3 -
Visuals
3 -
R script
3 -
Aggregation
3 -
Dataflow
3 -
calendar
3 -
Gateways
3 -
R
3 -
M Query
3 -
R visual
3 -
Webinar
3 -
CALCULATE
3 -
Reports
3 -
Visualization
2 -
Tabular Editor
2 -
Date
2 -
SharePoint
2 -
Power BI Installation and Updates
2 -
How Things Work
2 -
troubleshooting
2 -
Date DIFF
2 -
Transform data
2 -
rank
2 -
ladataweb
2 -
Tips and Tricks
2 -
Incremental Refresh
2 -
Query Plans
2 -
Power BI & Power Apps
2 -
Random numbers
2 -
Day of the Week
2 -
Number Ranges
2 -
M
2 -
hierarchies
2 -
Power BI Anniversary
2 -
Language M
2 -
Custom Visual
2 -
VLOOKUP
2 -
pivot
2 -
calculated column
2 -
Power BI Premium Per user
2 -
inexact
2 -
Date Comparison
2 -
Split
2 -
Forecasting
2 -
REST API
2 -
Editor
2 -
Working with Non Standatd Periods
2 -
powerbi.tips
2 -
Custom function
2 -
Reverse
2 -
measure
2 -
Microsoft-flow
2 -
Paginated Report Builder
2 -
PUG
2 -
Custom Measures
2 -
Filtering
2 -
Row and column conversion
2 -
Python script
2 -
Nulls
2 -
DVW Analytics
2 -
Industrial App Store
2 -
Week
2 -
Date duration
2 -
parameter
2 -
Weekday Calendar
2 -
Support insights.
2 -
construct list
2 -
Formatting
2 -
Power Platform
2 -
Workday
2 -
external tools
2 -
slicers
2 -
SAP
2 -
index
2 -
RANKX
2 -
Integer
2 -
PBI Desktop
2 -
Date Dimension
2 -
Power BI Challenge
2 -
Query Parameter
2 -
Showcase
1 -
custom connector
1 -
Waterfall Chart
1 -
Power BI On-Premise Data Gateway
1 -
step by step
1 -
Top Brand Color on Map
1 -
Tutorial
1 -
Previous Date
1 -
XMLA End point
1 -
color reference
1 -
Date Time
1 -
Marker
1 -
Lineage
1 -
CSV file
1 -
conditional accumulative
1 -
Matrix Subtotal
1 -
Check
1 -
null value
1 -
Report Server
1 -
Audit Logs
1 -
analytics pane
1 -
mahak
1 -
pandas
1 -
Networkdays
1 -
Button
1 -
Dataset list
1 -
Keyboard Shortcuts
1 -
Fill Function
1 -
LOOKUPVALUE()
1 -
Tips &Tricks
1 -
Plotly package
1 -
refresh M language Python script Support Insights
1 -
Excel
1 -
Cumulative Totals
1 -
Report Theme
1 -
Bookmarking
1 -
oracle
1 -
Canvas Apps
1 -
total
1 -
Filter context
1 -
Difference between two dates
1 -
get data
1 -
OSI
1 -
Query format convert
1 -
ETL
1 -
Json files
1 -
Merge Rows
1 -
CONCATENATEX()
1 -
take over Datasets;
1 -
Networkdays.Intl
1 -
Get row and column totals
1 -
Sameperiodlastyear
1 -
Office Theme
1 -
matrix
1 -
bar chart
1 -
Measures
1 -
powerbi argentina
1 -
Model Driven Apps
1 -
REMOVEFILTERS
1 -
XMLA endpoint
1 -
translations
1 -
OSI pi
1 -
Parquet
1 -
Change rows to columns
1 -
remove spaces
1 -
Azure AAD
1 -
Governance
1 -
Fun
1 -
Power BI gateway
1 -
gateway
1 -
Elementary
1 -
Custom filters
1 -
Vertipaq Analyzer
1 -
powerbi cordoba
1 -
DIisconnected Tables
1 -
Sandbox
1 -
Honeywell
1 -
Combine queries
1 -
X axis at different granularity
1 -
ADLS
1 -
Primary Key
1 -
Microsoft 365 usage analytics data
1 -
Randomly filter
1 -
Week of the Day
1 -
Get latest sign-in data for each user
1 -
Retail
1 -
Power BI Report Server
1 -
School
1 -
Cost-Benefit Analysis
1 -
ISV
1 -
Ties
1 -
unpivot
1 -
Practice Model
1 -
Continuous streak
1 -
ProcessVue
1 -
Create function
1 -
Table.Schema
1 -
Acknowledging
1 -
Postman
1 -
Text.ContainsAny
1 -
Power BI Show
1 -
query
1 -
Dynamic Visuals
1 -
KPI
1 -
Intro
1 -
Icons
1 -
Issues
1 -
function
1 -
stacked column chart
1 -
ho
1 -
ABB
1 -
KNN algorithm
1 -
List.Zip
1 -
optimization
1 -
Artificial Intelligence
1 -
Map Visual
1 -
Text.ContainsAll
1 -
Tuesday
1 -
API
1 -
Kingsley
1 -
Merge
1 -
variable
1 -
financial reporting hierarchies RLS
1 -
Featured Data Stories
1 -
MQTT
1 -
Custom Periods
1 -
Partial group
1 -
Reduce Size
1 -
FBL3N
1 -
Wednesday
1 -
help
1 -
group
1 -
Scorecard
1 -
Json
1 -
Tops
1 -
Multivalued column
1 -
pipeline
1 -
Path
1 -
Yokogawa
1 -
Dynamic calculation
1 -
Data Wrangling
1 -
native folded query
1 -
transform table
1 -
UX
1 -
Cell content
1 -
General Ledger
1 -
Thursday
1 -
Power Pivot
1 -
Quick Tips
1 -
data
1 -
PBIRS
1 -
Usage Metrics in Power BI
1 -
HR Analytics
1 -
keepfilters
1 -
Connect Data
1 -
Financial Year
1 -
Schneider
1 -
dynamically delete records
1 -
Copy Measures
1 -
Friday
1 -
Table
1 -
Natural Query Language
1 -
Infographic
1 -
automation
1 -
Prediction
1 -
newworkspacepowerbi
1 -
Performance KPIs
1 -
Active Employee
1 -
Custom Date Range on Date Slicer
1 -
refresh error
1 -
PAS
1 -
certain duration
1 -
DA-100
1 -
bulk renaming of columns
1 -
Single Date Picker
1 -
Monday
1 -
PCS
1 -
Saturday
1 -
Q&A
1 -
Event
1 -
Custom Visuals
1 -
Free vs Pro
1 -
Format
1 -
Current Employees
1 -
date hierarchy
1 -
relationship
1 -
SIEMENS
1 -
Multiple Currency
1 -
Power BI Premium
1 -
On-premises data gateway
1 -
Binary
1 -
Power BI Connector for SAP
1 -
Sunday
1 -
update
1 -
Slicer
1 -
Visual
1 -
forecast
1 -
Regression
1 -
CICD
1 -
sport statistics
1 -
Intelligent Plant
1 -
Circular dependency
1 -
GE
1 -
Exchange rate
1 -
Dendrogram
1 -
range of values
1 -
activity log
1 -
Decimal
1 -
Charticulator Challenge
1 -
Field parameters
1 -
Training
1 -
Announcement
1 -
Features
1 -
domain
1 -
pbiviz
1 -
Color Map
1 -
Industrial
1 -
Weekday
1 -
Working Date
1 -
Space Issue
1 -
Emerson
1 -
Date Table
1 -
Cluster Analysis
1 -
Stacked Area Chart
1 -
union tables
1 -
Number
1 -
Start of Week
1 -
Tips& Tricks
1 -
deployment
1 -
ssrs traffic light indicators
1 -
SQL
1 -
trick
1 -
Scripts
1 -
Extract
1 -
Topper Color On Map
1 -
Historians
1 -
context transition
1 -
Custom textbox
1 -
OPC
1 -
Zabbix
1 -
Label: DAX
1 -
Business Analysis
1 -
Supporting Insight
1 -
rank value
1 -
Synapse
1 -
End of Week
1 -
Tips&Trick
1 -
Workspace
1 -
Theme Colours
1 -
Text
1 -
Flow
1 -
Publish to Web
1 -
patch
1 -
Top Category Color
1 -
A&E data
1 -
Previous Order
1 -
Substring
1 -
Wonderware
1 -
Power M
1 -
Format DAX
1 -
Custom functions
1 -
accumulative
1 -
DAX&Power Query
1 -
Premium Per User
1 -
GENERATESERIES
1